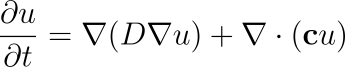Diffusion Convection Equation

Diffusion Convection Equation#

Introduction#

The Diffusion Convection Equation is a Partial Differential Equation writen in the form:

\[\frac{\partial u}{\partial t} = \nabla ( D \nabla u) + \nabla \cdot (\mathbf{c} u)\]

This Equation can model most physical phenomena involving the transfer of a quantity by ‘Diffusion’ and ‘Convection’ (Advection).

  1. \(\nabla(D \nabla u)\) is the diffusion term. Diffusion describes the net movement of a quantity \(u\), generally from a region of higher concentration to lower concentraction.

  2. \(\nabla \cdot (\mathbf{c} u)\) is the convection term. Convection (Advection) describes the bulk motion of a quantity \(u\) under the a velocity field \(\mathbf{c}\).

Click here for more information on the Diffusion Convection Equation.

Simplifications#

There are a number of simplifications made to this model.

  1. Let the diffusion coefficient \(D\) be constant, this means it can come outside of the gradient operator resulting in the dot product of the gradients becoming the Laplacian. Hence the diffusion is written as \(D \nabla^2 u\).

  2. Let the convection vector field be constant, this means the convection term siplifies to \(\mathbf{c} \cdot \nabla u\).

Diffusion Equation#

Suppose a model where \(\mathbf{c} = 0\). This can be interpreted as a quantity \(u\) under going diffusion only, so \(u\) is not flowing with any vector field. instead it is moving into the less concentrated areas. This model is governed by the following Partial Differential Equation:

\[\frac{\partial u}{\partial t} = D\nabla^2 u\]

Convection Equation#

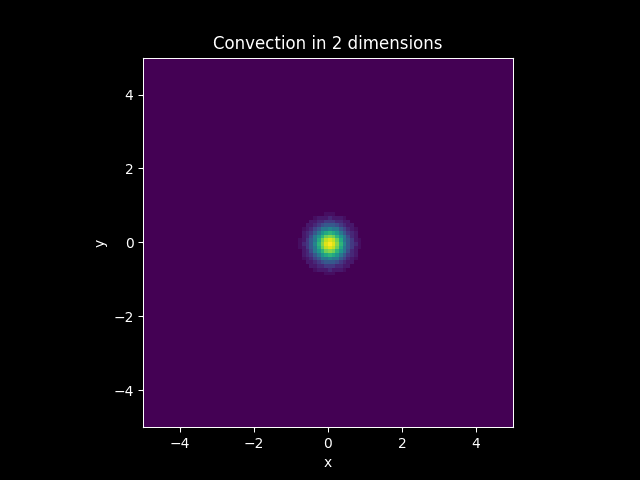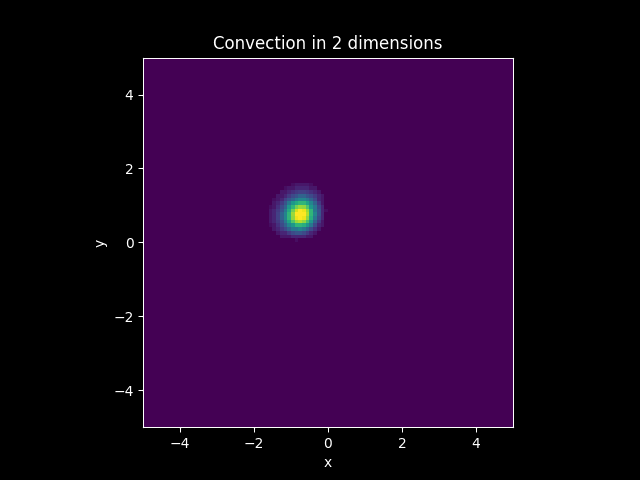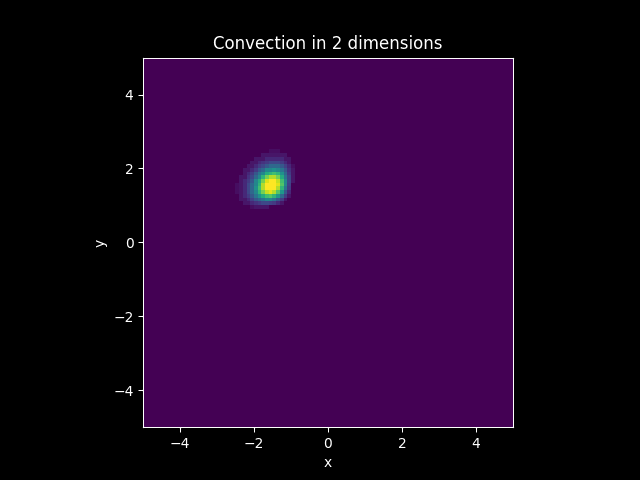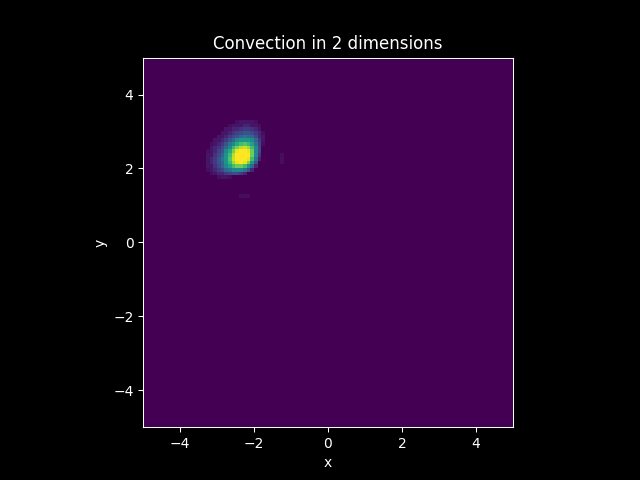
Suppose a model where \(D = 0\). this can be interpreted as a under going convection only, so \(u\) is being transported with the same density distribution by a constant vector field \(\mathbf{c}\). This model is governed by the following Partial Differential Equation:

\[\frac{\partial u}{\partial t} = \mathbf{c} \cdot \nabla u\]

Examples#

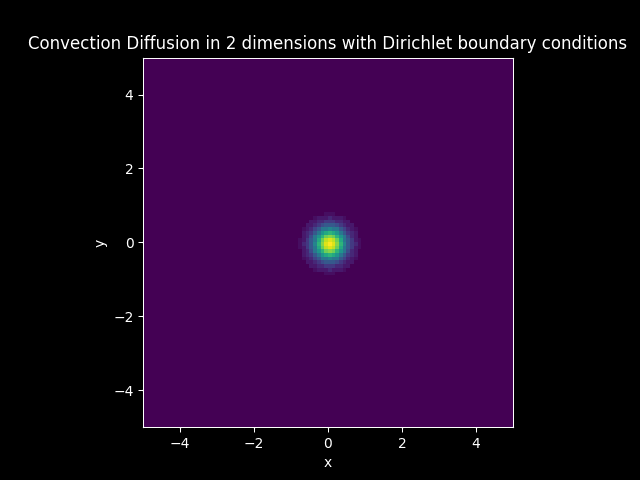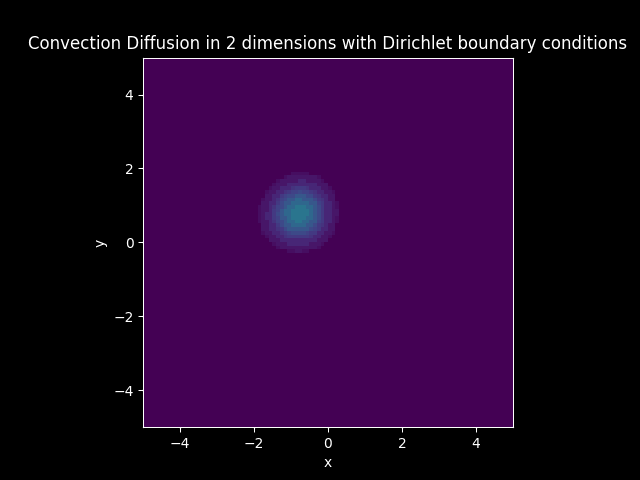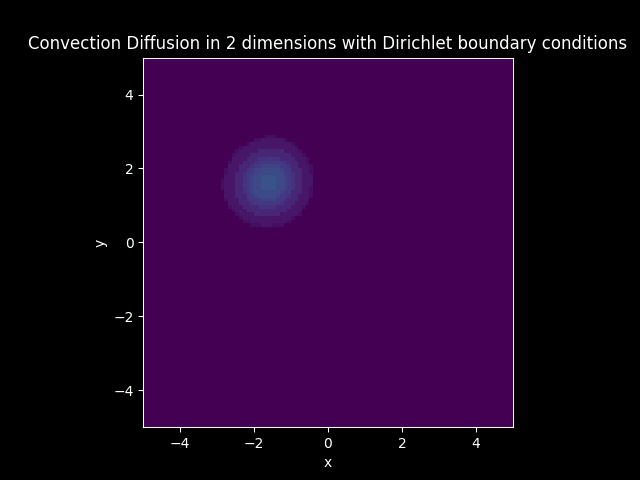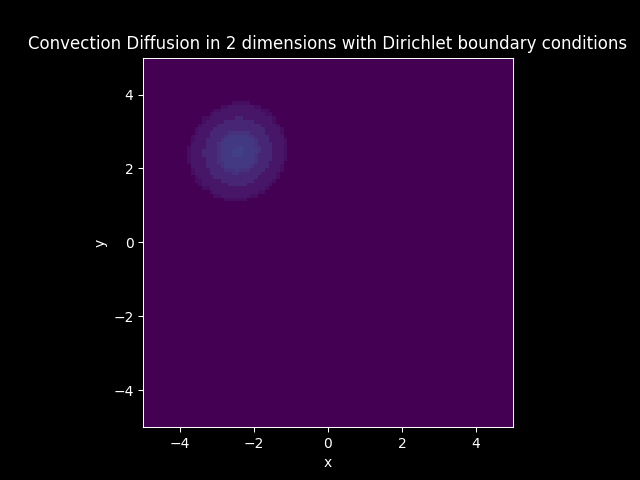
Consider a Diffusion Convection model in 2 dimension with the vector \(\mathbf{c}\) having equal vector components and \(D\) is constant.

Let \(\mathbf{c} = [-0.1, -0.1]\) and \(D = 0.009\). (Neumann boundary condition and 3d animations can be found in Two dimensional examples)

Diffusion Convection Model#

Solution:

Diffusion Model#

Solution:

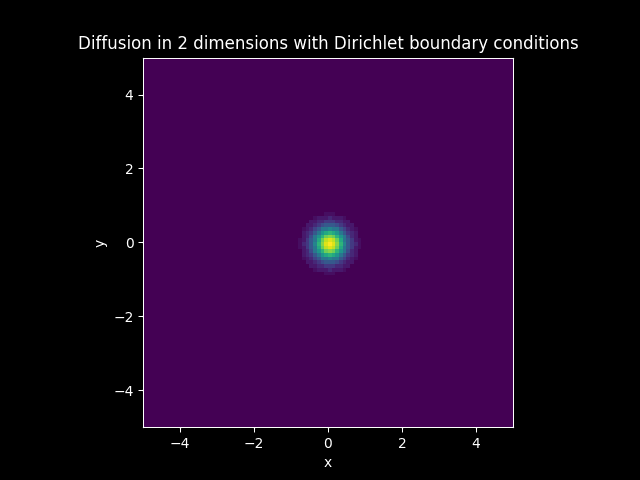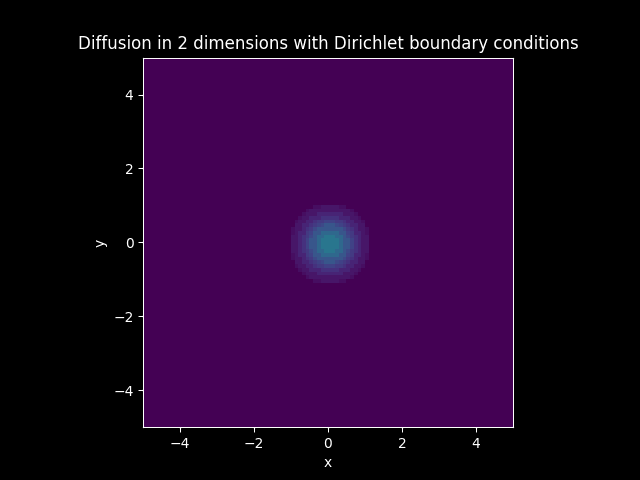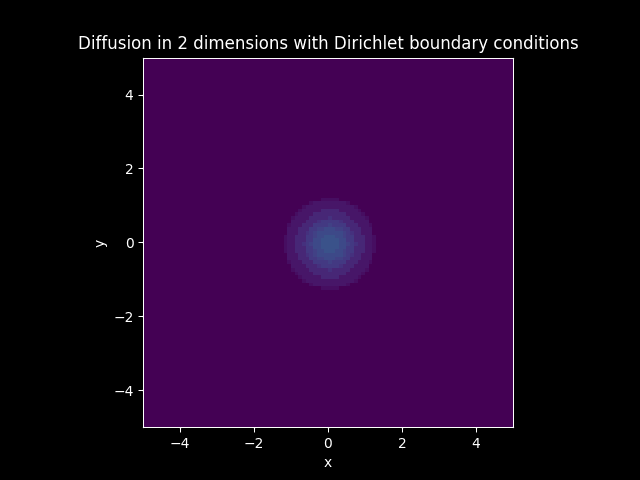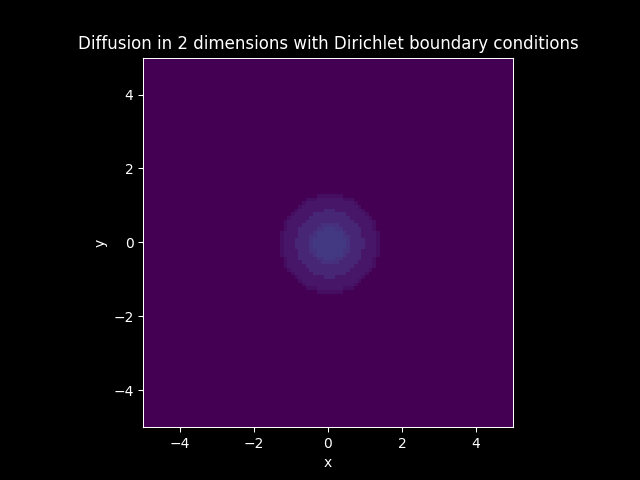
Convection Model#

Solution:

Applications#

Some applications of these models include:

  1. Heat Transfer or cooling of a system.

  2. Tranportation of a fluids density distribution that is flowing uniformly.

  3. Fokker Plank Equation of a Stochastic Differential Equation with uniform drift and standard deviation.